Fibonacci in human grammar
In my first week of graduate school, I noticed a minor mathematical curiosity, which would grow into something of an obsession. My advisor, Andrew Carnie, had mentioned that Juan Uriagereka was working on Fibonacci patterns in language. Andrew recommended Juan’s book Rhyme and Reason, but the library’s only copy was checked out at the time.
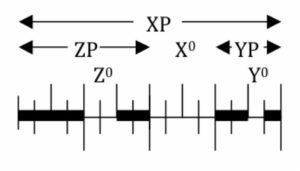
Frustrated, I went home and tried to work out what he might have been talking about. Playing around with what little syntax I knew at the time, I noticed that the X-bar schema of Phrase –> [Specifier-Phrase [Head Complement-Phrase]], if iterated indefinitely, produced the Fibonacci numbers, in the numbers of each type of bar-level object in successive generations.
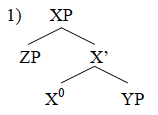
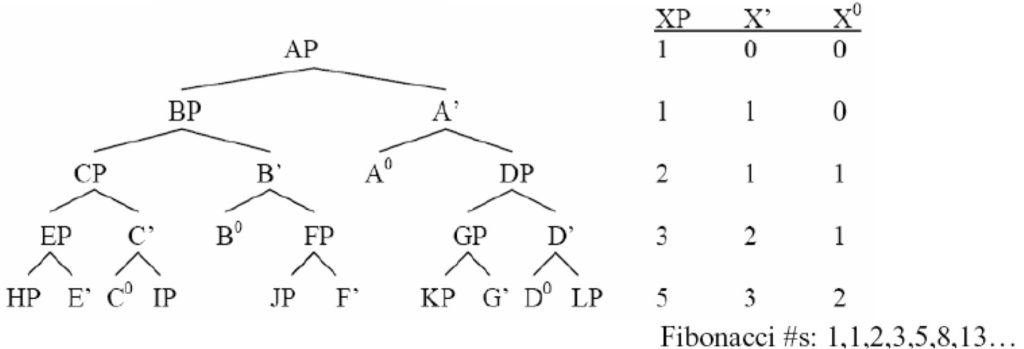
The next day, I told Andrew that I had guessed what Juan must have been talking about. Andrew looked at my scribbled diagram and told me Juan had something else in mind, but what I saw might be interesting. At the time (2005), it seemed like a promising lead, given the Zeitgeist of biolinguistics and third factors. The idea, mere hand-waving at the time, was that Fibonacci patterns in syntax might arise as something like an optimal packing solution, determined by natural law rather than anything specific to language. On the face of it, it seemed at least plausible, as related mathematics seems to arise in a variety of surprising places in nature (organic and inorganic) — the kind of thing that Alan Turing was referring to when he said “some physical processes are of very general occurrence.”

[Image from http://britton.disted.camosun.bc.ca/fibslide/fib31.gif]
Andrew and I wrote a short paper together, trying to spin the observation into saying something about the EPP (the Extended Projection Principle — the rather mysterious requirement that sentences must have surface subjects, even if they don’t have logical subjects). Hearing that Cedric Boeckx had written something about the size of phases relating to Fibonacci numbers, we folded in his work as well in another paper (the former was published in a working papers volume; the latter never got beyond manuscript stage).
What kind of optimization matters for sentences?
In presenting this work in the department, another student (the brilliant Roeland Hancock) asked me a question that led me to my thesis project: if the X-bar pattern really is optimal, what is it optimal with respect to? In phyllotaxis, the pattern arises as a consequence of physical concerns (involving differential absorption of the morphogen auxin in the shoot apical meristem); what “forces” were at work in language that might lead to the same solution?
The best answer I could find had to do with computational concerns: namely, minimization of c-command relations, which meant minimizing search space over the course of a derivation. Exploring that idea led to my first major publication, Optimal Growth in Phrase Structure, and eventually became part of my dissertation work, described in the Economy of Command section.
Other explanations for Fibonacci syntax
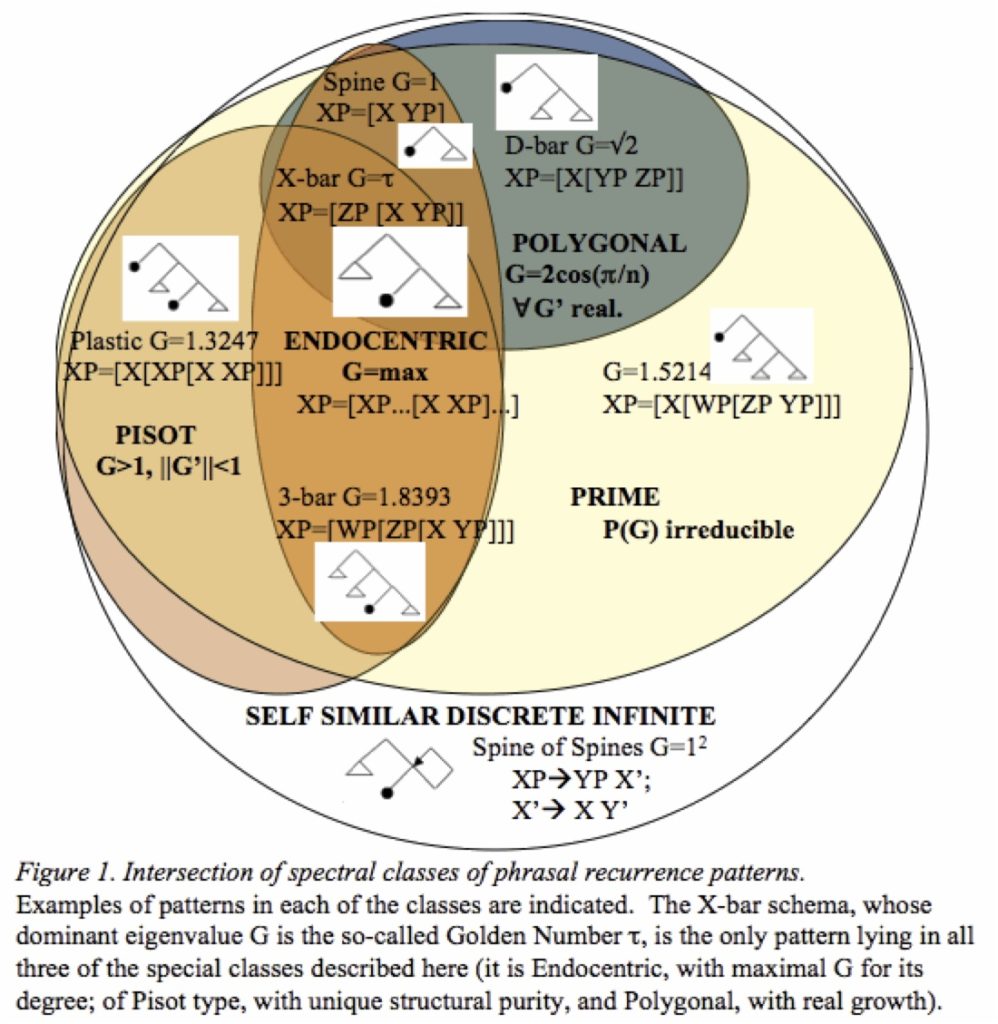
Nevertheless, I kept thinking about other ways to explain what seemed to me like a potentially important observation. The line I took was to conceive of the X-bar schema as a self-similar template for recursive structure, and to compare its properties to the properties of other self-similar recursive templates. This led me to thinking about L(indenmayer)-grammars, and quasiperiodicity (as in the famed Penrose tilings), and some interesting algebraic properties of X-bar syntax as L-grammar. Most of what I explored went nowhere, but the algebraic stuff (based on formulating the pattern as a matrix, and comparing it to the matrix form of other conceivable structural templates) grew into a book chapter with Massimo Piattelli-Palmarini, The Golden Phrase, accepted but (as of early 2017) still awaiting publication. We pointed out that a number of quite interesting and, maybe, “desirable” properties converge uniquely in the X-bar format.
Other linguists were interested in Fibonacci numbers, and the closely related golden mean, for their own reasons. Doug Saddy and his group, at the University of Reading, have done a fascinating series of experiments showing a special behavioral response to the Fibonacci L-grammar realized as an auditory sequence, vis-a-vis superficially similar sequences, and distinct L-grammar sequences (such as the Thue-Morse Grammar). Tom Bever had some experimental results showing a special role for golden-mean rectangles in enhancing the perception of a variety of visual illusions. Tom has an idea that syntactic movement is related in some way to the visual perception of actual movement, and he egged me on in pursuing my decidedly eccentric ideas.
Where to go from here?
I’ve largely abandoned this line of research. I still think there’s something interesting to be found, somewhere down this rabbit hole, but I’ve found more promising ideas to chase. Someday, if time permits, I might like to return to these ideas and try to do something substantive to explore them. For example, inspired by Saddy’s experiments, I created draft experimental stimuli (for which Dan Brenner generously created a Praat script) to explore the algebraic properties Massimo and I speculated about in our paper. The idea is to probe the behavioral response to L-grammars with more or less of the special properties that come together in the X-bar-like Fibonacci L-grammar. Slides with embedded audio files are here: stimuli samples.
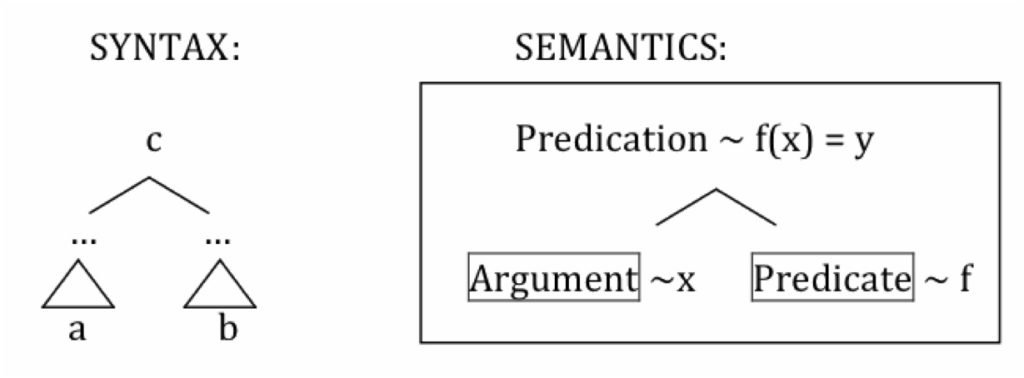
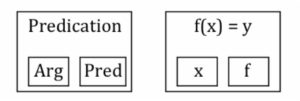
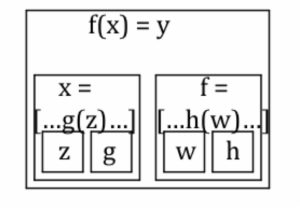
Another interesting point (noticed, and abandoned) is that the X-bar format provides what I came to think of as a “minimal semantic generator”. Suppose that we are trying to find a single structural template for expressions, with the following conditions. First, it must allow us to express predicates and arguments, and provide a way to distinguish them in structural terms. Second, we want predicates and arguments to each potentially contain further predicate-argument structure. Let’s further limit the options to binary branching. Then it turns out that the X-bar schema is the simplest structural format that meets our requirements. Moreover, any more complicated scheme does not add additional expressive power — any expression built with a higher-order template can be “Schoenfinkelized” into an equivalent expression built from the X-bar form.
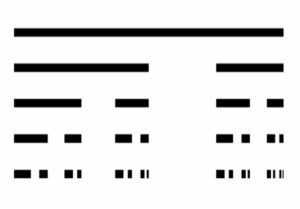
If anyone wants to poke around in the rabbit hole themselves, I have some old slides bringing together a variety of strands of my research on this topic here: FibXbar Compendium. These provide more detail on most of what is mentioned above, and a good deal more: further ways of finding Fibonacci numbers in X-bar trees; the X-bar scheme as a description of an asymmetric Cantor set, the simplest kind of multi-fractal (see images below); X-bar as a good solution for “cephalotaxis” (growing as many heads/terminals as possible for a fixed tree depth), and so on.