My current project is ULTRA: the Universal Linear Transduction Reactive Automaton (formerly called QLSR: Queue Left, Stack-sort Right). This project aims to develop a radically new model of syntax, in the form of a universal-parser-as-universal-grammar.
Origins of ULTRA
The seeds of these ideas first sprouted in late 2014, and developed considerably during the spring semester of 2015. I had been hired to teach a graduate Topics seminar, ostensibly on my thesis material… but I ended up working through the ideas described below, and presenting them to the class each week for discussion. A number of the graduate students from that class joined my informal QLSR research group to continue to work on these ideas. This grew a few offshoots: for example, during Spring 2016, I supervised Ray Daniels’ internship project in the Human Language Technology master’s program, for which he created a proof-of-concept parser to implement the developing theory. I also presented a poster (PDF) on the treatment of Universal 20 with Ryan Walter Smith at the annual LSA meeting in January 2017.
Catalan numbers in word order universals
As mentioned at the end of my Economy of Command page, one day I noticed something strange in Cinque’s account of Universal 20, which concerns the cross-linguistic ordering of demonstrative, numeral, adjective, and noun.
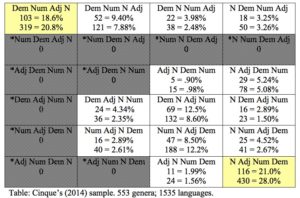
Cinque’s account of possible and impossible orderings posits a fixed universal order of external Merge (the noun combines with the adjective first, then the numeral, and then the demonstrative), and a constraint on movement: any instance of Internal Merge must move the noun (or something containing it) to the left; so-called remnant movement is barred. Cinque’s scheme allows 2 possible orders of 2 elements; 5 possible orders of 3 elements, 14 orders for 4 elements, 42 orders for 5 elements…
These are the Catalan numbers, which show up in too many guises to count in combinatorics. Among many things counted by the Catalan numbers are the Dyck trees of successive sizes (which are simply the set of all distinct ordered, rooted trees).
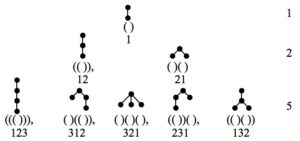
It turns out that there is a straightforward mapping between the trees described by Cinque’s non-remnant-moving derivations, and the Dyck trees (see below). That’s weird already: it suggests that one can generate his trees directly, without bothering with a syntactic derivation involving movement.
Permutations avoiding forbidden subsequences & stack-sorting
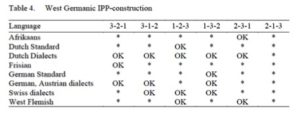
Reading some more about these topics, I ran across the notion of permutations avoiding a forbidden subsequence (permutations avoiding a given 3-item subsequence are also counted by the Catalan numbers). Now, this applies directly to the kinds of word order facts Cinque was examining, and has been explicitly recognized in work on related facts in verb clusters. For a verb cluster with elements 1, 2, 3 indicating greater depth of embedding, it has been noted that while all other permutations of order are possible (in various related dialects), the order 213 seems to be systematically avoided. For example, the table below is taken from Wurmbrand (2015); the point is that the elements of an IPP construction (one of several flavors of verb cluster) can be expressed, in some West Germanic language, in any order… except *213.
A final piece of the puzzle fell into place when I encountered Donald Knuth’s stack-sorting algorithm (which can sort only some permutations, and not others). Traditionally,the permutations that can be properly stack-sorted are described as 231-avoiding. However, linguists in effect number their trees upside down: what we record as a 123 sequence is meant to be semantically composed in the order 321 (i.e., bottom-up). This meant that Cinque’s attested noun phrase orders, and attested verb cluster orders, were all and only the stack-sortable permutations of the universal composition order. So… stack-sorting, deployed as a parsing algorithm, would sort all and only the attested word orders into their universal bottom-up interpretation.
Stack-sorting algorithm Definitions
While input is non-empty, I is the next item in input.
If I » S, Pop. S is the item on top of the stack.
Else Push. x » y if x c-commands y in the base (e.g. Dem » N).
While Stack is non-empty, Push moves I from the input onto the stack.
Pop. Pop moves S from the stack to the output.
Parsing by stack-sorting
So, stack-sorting is an effective procedure to get from word order to hierarchical order (note: without mediation of an autonomous grammar). That’s interesting in itself, but there’s more. Not only did the stack-sorting algorithm get the right interpretation for all and only the attested word orders; it also got the right structures. Remember the Dyck trees mentioned above? Reading the storage step (from word order to memory) as a left bracket, and the retrieval step (from memory to interpretation) as a right bracket created exactly the Dyck trees… in each case corresponding to the binary tree(s) describing the Cinque derivation(s) for that word order. It’s natural, moreover, to take the element stored or retrieved as the “label” of the associated bracket: so, that’s unambiguous, zero-search labeling.
Taken together, this process folds together linearization, displacement, composition, surface-structure bracketing, and labeling of those brackets, into a single real-time performance process. Which also explains a class of word order universals, and eliminates the derivational ambiguity that haunts Cinque’s account of the facts (more on that below). It does this with a universal parsing algorithm, identical for all languages, with no parameters or features driving movement. And… it also dispenses with Merge (I’ll delve more into that as well).
Demonstration of stack-sorting
Unless you’re a computer scientist, this is probably quite opaque up to this point. I’ve found, in talking about this over the past few years, that when I try to describe the idea, most people stare at me like I’m some strange bug… until I visually demonstrate the process, at which point it instantly “clicks”. In early talks I used a pile of books of different colors to illustrate; then I took to carrying around with me a set of my kids’ MegaBloks with noun phrase elements written on them. (“My theory is about the basic building blocks of language…”)
up to this point. I’ve found, in talking about this over the past few years, that when I try to describe the idea, most people stare at me like I’m some strange bug… until I visually demonstrate the process, at which point it instantly “clicks”. In early talks I used a pile of books of different colors to illustrate; then I took to carrying around with me a set of my kids’ MegaBloks with noun phrase elements written on them. (“My theory is about the basic building blocks of language…”)
Eventually I created the animations embedded below (click on the movies to watch them play).
The video above shows how stack-sorting applies to each possible permutation of an abstract hierarchy (numbered in the linguistic convention, such that a “1” is the highest element in the base hierarchy, while “3” is the lowest). We begin with a surface word order, represented as a stack of blocks, which will be taken off one-by-one and moved to the stack in the middle, and from there to the output on the left. At various points, we will have a choice whether to move the next input item to the stack, or the current top-of-stack to the output. This choice is governed by Knuth’s stack-sorting algorithm. In this application, if the next input item has a higher number (i.e., is supposed to be deeper in the base hierarchy), it is moved to the stack; if the stack item has a larger number, instead move it to the output. (I draw a blue box and a < or > symbol to indicate which way the comparison between input and stack items goes when it occurs).
As you can see, all of the permutations except 213 are stack-sorted into a uniform output, arriving there in the desired bottom-up order 321. Thinking of this in terms of linguistic hierarchies (I flash some images at the end making this explicit), this means any surface word order, save a 213-containing permutation, gets sorted by this procedure into its notional “base” order — i.e., the bottom-up order of composition. In a way, we’re reversing the directionality usually assumed in generative explanations, where the base order effectively comes first (built by External Merge), and work must be done (by movement, Internal Merge) to put things into their surface positions. Things flow the other way here, from whatever permutation is encountered in the surface word order, to the interpretation as the end point.
Stack-sorting Universal 20
Watching 6 stack-sorting procedures, applying to an abstract hierarchy, all unfold at once might be less than crystal-clear. The videos below demonstrate how stack-sorting applies to some individual attested noun phrase orders (and one unattested order).
Stack-sorting head-initial DP order (English)
Above, we start with the English word order for the categories relevant to Universal 20, these three blind mice. As you can see, everything piles into the stack, then everything comes back out in reverse order, correctly yielding the bottom-up interpretation “mice blind three these”.
Generative syntax has sometimes been accused of being Anglo- or Euro-centric: the “base” often looks suspiciously like English, or Italian, etc. So perhaps it’s comforting that in this system, the English order is in a sense the most perverse — everything has to pile into memory before anything is interpreted. (If you’re yelling at your monitor right now, “That can’t be right, what about incremental interpretation?!” …bear with me, I’ll get there.)
Stack-sorting head-final DP order (Thai, Maori, etc.)
Above I demonstrate the stack-sorting of the mirror image of the English order, mice blind three those. Things are particularly simple here; in a sense we don’t even need memory, as the surface order just is the interpretation order. Note that this is actually the most common order across the world’s languages, more common than the next-most common order, which is the English pattern. The memory-less-ness of this order will come back in the later discussion on the preference for suffixes over prefixes across languages, and why that preference varies with the overall clause order of a language.
Stack-sorting Basque DP order
Basque has lots of odd properties. But at least in terms of stack-sorting, we may be reassured to discover that its surface DP order, three mice blind those, is indeed stack-sorted into the hypothesized universal bottom-up order, like all other attested orders.
Stack-sorting an unattested order
Now for the punchline: watch what happens when we feed one of the unattested DP orders (here, blind those three mice)* into our stack-sorting procedure. The algorithm chugs along, following the same rules at each step as in the other examples: PUSH (input to stack) if input > stack; POP (stack to output) if input < stack. But notice that the end result is different: the output order is not the desired universal order of bottom-up interpretation. Instead, we have a putative noun phrase with an adjective at the bottom. By assumption, that’s not a possible interpretation, and that is why ULTRA rules out this order (and other 213-containing permutations).
Aside: Note that 3124 counts as a 213-containing permutation. This may seem confusing at first: what’s ruled out is any permutation that has a …mid…high…low… contour (low, mid, high referring to positions in the interpretive hierarchy), possibly interrupted with other elements. So, the 3…1…4 subsequence is what makes this count as a 213-containing permutation.
*One can find orders like this in Slavic languages. But crucially, they’re not information-neutral orders: the adjectival element is interpreted as focused in such orderings. We’ll come back to why that’s important, and how to handle such apparent exceptions, down below.
An aside: crossing dependencies with a stack
Stack-sorting is a form of linear transduction. Historically, linear transduction has been largely ignored as a possible model of grammar. As a consequence, there are some surprises lurking here for usual ways of thinking about formal properties of language.
Together with the kinds of rewrite systems usually deployed for describing syntactic structure, there are a set of well-understood parsing approaches implementing various kinds of grammars. This can be related to the familiar Chomsky Hierarchy of formal languages. One familiar result relates the kind of memory available to a parser to the Chomsky hierarchy. So, a regular language can be parsed without memory, by a finite-state automaton. A context-free language, characterized by nesting dependencies among elements, can be parsed by a push-down automaton, with stack memory. Context-sensitive languages have crossing dependencies, and require memory beyond a single stack.
In this regard, it is perhaps surprising to note that stack-sorting can capture crossing dependencies. For example, both 4132 and 4231 are attested as noun phrase orders in Cinque’s sample (N-Dem-Adj-Num and N-Num-Adj-Dem, respectively). Both orders exhibit what would traditionally be considered crossing dependencies: in 4132, the dependency between the 3 and the 4 crosses the dependency between the 1 and the 2, and similarly in 4231 order. This matches the fact that such orders are treated as having movement, over and above basic phrase structure, in Cinque’s system as well as in Abels & Neeleman’s (2012) account, which allows free ordering of sister nodes. Likewise, a standard SR (shift-reduce) parser, with stack memory and a set of rewrite rules, could not parse these orders without extra technology.
Treating parsing as transduction changes the picture, though. Here, we can parse such orders easily with a single stack. Note that we’re not deploying rewrite rules either, a significant property I’ll return to below. For now, I’ll hint at what it means: we can have a single, unparameterized grammatical device, the same for all languages. Put another way, on this view there is only one I-language (interpretation order) and a uniform performance grammar (stack-sorter) that delivers it. More narrowly, it indicates that stack-sorting can handle local displacement: things that compose together in the interpretation need not be adjacent in the surface order.
How stack-sorting gets labeled brackets, without a competence grammar building trees.
Cool, so we have a new approach to Universal 20, which can be extended to verb cluster orders. If we think of a clause as a projection of a verb at the bottom, combining first with an object, and later with a subject, stack-sorting can parse any permutation of S, O, and V except OSV. That’s interesting, as OSV order as a basic clause order is vanishingly rare; of about 1400 languages described as having a dominant clause order in WALS, only 4 are claimed to have OSV basic order.
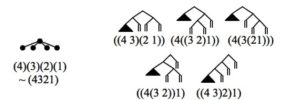
But beyond capturing word order facts, this approach also seems to get us very nearly the same trees that Cinque’s derivations generate, without the intervention of a competence grammar to build those trees with Merge. Let’s walk through how this works. Below, I provide in tabular form the complete stack-sorting computations for all possible permutations of a three-element hierarchy.
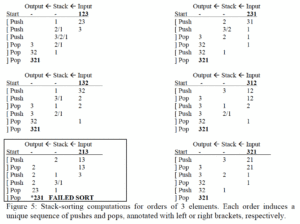
Stack-sorting has two operations: PUSH, moving an element from input to stack, and POP, moving an item from stack to interpretation. In familiar terms, these steps are storage and retrieval. I claim that storage (PUSH) is what linguists have been recording with left brackets, and retrieval (POP) is what a right bracket means. In the table, I’ve written a left or right bracket as appropriate next to each operation.
Now, let’s look at those brackets. Implicitly, brackets define a tree; as we see, what the brackets for the five stack-sortable permutations of three elements describe are exactly the Dyck trees (i.e. all possible ordered rooted trees) with 4 nodes. Storage (PUSH) and retrieval (POP) apply to a single element parsed from the input stream; it’s natural to take the element being manipulated to be the label of those brackets.
Let’s compare the brackets that emerge from stack-sorting these orders to those that describe Cinque’s remnant-avoiding derivations.

A few comments are in order at this point. A first point is that the ULTRA brackets are largely identical to the brackets in Cinque’s structures. But there are two differences, one conceptual/technical, the other with real empirical bite. Before we get there, though, let’s establish the correspondence a little more fully. What follows are, first, a table with all stack-sorting computations for all permutations of 4 elements – one can verify directly that this reproduces Cinque’s report of attested and unattested noun phrase orders, in that all and only the permutations corresponding to those orders get stack-sorted into the bottom-up composition order; all unattested orders yield a deviant output.
Again, we can read the PUSH operations as left brackets, and POPs as right brackets (labeled by the element they apply to). This implicitly describes a set of trees: again, the Dyck trees, this time over 5 nodes. In the table below, I collect in each cell: at top, the relevant order, as a permutation of 1234 and an order of Dem, Num, Adj, N; on the left, the PUSH-POP bracketing and the corresponding Dyck tree, and at right, the Cinque-style tree(s) — several orders have multiple derivations in his system, and so multiple tree representations.

Bracketing difference 1: words aren’t terminals
In the standard syntactic technology, words (or morphemes…) correspond to terminals in a (generally binary-branching) tree structure. The non-terminal nodes joining up constituents have a label, related in some way to their terminal contents. This relation, from terminals to non-terminal labels, is famously problematic; it’s one reason I thought my Economy of Command work was interesting, as it suggested a new kind of emergent solution.
In ULTRA, although we get basically the same brackets, when we read those brackets as trees we effectively discard the assumption that words (or morphemes) are terminals. Instead, they map onto any node in the Dyck tree (save the root). That’s interesting, since a similar technical move has been suggested independently, for example by Starke and Jayaseelan. To illustrate how this works, below left is the tree structure for 132 order, with the 1, 2, 3 written on the nodes. To its right is the kind of tree Cinque would have for the same order (the double vertical bar represents a constituent consisting of a head and a trace of movement; the dark triangle is the 3, the lexical bottom of the hierarchy which must be affected by any movement).

Bracketing difference 2: not strictly binary, and unambiguous
There’s another, very important difference between these new brackets and Cinque-style brackets. In Cinque’s system (as for most modern syntactic work), trees are binary-branching; this property is also thrown out in the brackets I derive, which besides binary-branching allow unary-branching as well as ternary-branching and beyond.
Closely related to this fact, Cinque’s system allows several derivations of certain orders (playing a little fast and loose; see below). For example, 321 surface order can be derived in two different ways. In one possible derivation consistent with his assumptions, the 3 inverts with the 2 as soon as the latter is Merged, and then the 32 complex inverts as a whole to the left of the 1 after the 1 is Merged. Alternatively, movement might not begin until the 1, 2, and 3 are present, at which point the 23 complex inverts left of the 1, and then the 3 is subextracted and moves by itself further left. (Some might object to such subextraction, referring to by a “freezing principle”, barring extraction from something that has already moved. However, subextraction of exactly this sort is required to derive noun-demonstrative-adjective-numeral (4132) order, which Cinque asserts to be attested).
This is where a crucial empirical difference emerges between ULTRA and Cinque’s account. In ULTRA, any single-domain surface order induces a unique sequence of parser actions, automatically. The relevant sequence for 321 order is Push3-Pop3-Push2-Pop2-Push1-Pop1; reading that as brackets, it’s [3 3] [2 2] [1 1], which amounts to a ternary-branching tree. In fact, wherever Cinque’s system allows multiple binary-branching derivations, ULTRA produces a single beyond-binary bracketed structure. The figure below compares the unambiguous, ternary-branching bracketing that ULTRA assigns to 321 order (at left), while at right are the two possible Cinque-style trees (again, a double vertical bar is a head and trace constituent, and the triangle is the 3 — the bottom of the hierarchy).
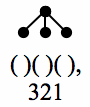
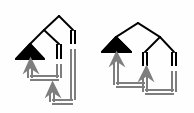
This difference matters. One of the reasons that constituency is treated as an axiom of syntax, by nearly everyone who has studied it, is that several converging lines of evidence convince us that brackets have some reality beyond notational convenience. For example, constituents delineated by matching brackets are thought to be the objects that undergo movement; brackets play a role in determining the domain of application of phonological effects like liaison and stress assignment, they enter into the determination of prosody, and so on.
So: Cinque’s account predicts that for some orders, there is a further layer of variation (associated with distinct derivations, leading to different bracketing). ULTRA predicts, in contrast, that each within-domain ordering has a single bracketed structure. This comes to a head with orders like noun-adjective-numeral-demonstrative, where Cinque’s system would allow up to five distinct derivations… and so, five varieties of language with this noun phrase order, detectable in subtle differences in terms of subextraction possibilities, phonological liaison, prosody and so on. Luckily, this order is also the most common noun phrase order across languages, so it should be straightforward to gather data to determine whether there are up to 5 varieties, or only a single “flat” (quaternary-branching) structure as predicted here.
An aside on labeling
If you’re familiar with Chomsky’s Labeling Algorithm, based on minimal search and sometimes ambiguous, you may be interested to note that the labeling that comes out of stack-sorting amounts to a zero-search, unambiguous labeling algorithm. You may worry that this is a bad thing; Chomsky appeals to ambiguity in his Labeling Algorithm to account for forcing movement from unlabelable structures (a la Moro’s Dynamic Antisymmetry), as well as to describe where movement stops (adopting Rizzi’s Criterial Freezing). So I’ll need a different story about the relevant effects… we’ll get there; bear with me.
A further point concerns the labels I indicate in Cinque-style derivations. Technically, in Cinque’s theory the (non-bottom) elements aren’t heads, which could label the phrase containing them. Instead, in line with Kayne’s Linear Correspondence Axiom, he has them as phrasal specifiers of silent functional heads. So it is a bit of an oversimplification on my part to say that modifiers in the noun phrase directly label the brackets containing them. But it’s a very short step from Cinque’s machinery, where the brackets are still for the relevant elements, though somewhat indirectly; in Cinque’s view the labels come from silent functional heads associated with the modifiers, not the from the overt modifiers themselves.
One more bit of technical clarification: I am oversimplifying Cinque’s story in another way as well. For him, the landing sites of movement are provided by further (generally phonologically inert) layers of structure, in the form of dedicated Agreement Phrases above each modifier-introducing category. This might reduce somewhat the full range of movements I claim to be possible in his system. But it should be clear that these AgrPs are clutter induced by trying to comply with Kayne’s LCA, rather than a central part of his theory. Put another way, nothing would prevent the postulation of further layers of silent structure to host further movement (or one could appeal to multiple adjunction/multiple specifiers to host such movements). See, for example, Abels & Neeleman (2012).
Why Harmonic orders are special
The attested noun phrase orders are not at all evenly distributed in terms of typological frequency; some are overwhelmingly more common than others. In particular, so-called Harmonic ordering (strict head-initial or head-final ordering) accounts for almost half of the sample. It seems that this is not an accident: artificial grammar learning experiments, by Jennifer Culbertson and colleagues, suggest that such orders are easiest to learn — apparently regardless of the native language of experimental subjects.
Cinque suggested a way of capturing the typological distribution, in terms of relative markedness of derivational options. But the markedness of each option is ad hoc, stipulated so as to capture the facts, rather than explaining them.
It turns out that there is a nice explanation for the preference for Harmonic ordering in ULTRA. For simplicity, let’s consider just the ordering of three elements (1, 2, 3). As we’ve seen already, there is something particularly straightforward about parsing 321 order with ULTRA: the surface order matches the interpretation order, and no reordering is required.
123 order is, by the same metric, in a sense the “worst” order: everything has to pile into memory before the interpretation can be constructed by pulling everything out, in reverse order. But this, it turns out, is actually an advantage — not for memory, but for learning.
Imagine the plight of a child, confronting an unknown language in their environment. By assumption, the proper hierarchical ordering is innate (more on this below); the child’s task is to properly map categories in the surface order to this innate hierarchy, which is not trivial. Assume, furthermore, that the child can identify the bottom of the hierarchy (the 3, in this case), in some reliable way. This is not entirely unreasonable, as this is the position of the lexical bottom of a functional sequence, and is plausibly special in terms of statistical and phonological properties.
For 123 order, the very fact that everything else had to pile into stack memory in advance of the lexical bottom means that the learning problem is solved. That is, there is no choice in how to retrieve the other elements (1 and 2): they must be retrieved in last-in, first-out order, due to the stack memory structure. This is not the case for any of the other attested orders (132, 231, and 312). To interpret those orders correctly, the child must have learned their relative hierarchy independently, to determine their proper order of retrieval.
Stack-sorting morphology: The suffixing preference, and its correlation with clause order
A well-known fact is that, across languages, there is a considerable preference for suffixes over prefixes (simply counting them, we find about three times as many suffixes as prefixes). This has been discussed in terms of processing effects before. For example, Cutler, Hawkins & Gilligan suggest that there is a pressure to identify words as quickly as possible. Prefixes, because they are less distinctive than the stems to which they attach, tend to delay the identification of unique words. Suffixes, on the other hand, because they follow stems which are more distinctive, allow earlier identification of unique words.
However, there is a further layer to the typological facts: the suffixing preference correlates significantly with overall clause order. SOV languages tend to be almost exclusively suffixing, with about a 5-to-1 ratio of suffixes to prefixes. SVO languages prefer suffixes more weakly, at about a 2-to-1 ratio. Verb-initial languages, on the other hand, seem to allow prefixes still more freely, with about even numbers of suffixes and prefixes.
ULTRA suggests an interesting possible analysis of this set of facts. Let us adopt the common view that morphology is computed with the same system that does syntax: here, that means that individual morphemes are stack-sorted into their interpretation order.
First, we can justify the overall preference for suffixes over prefixes in the same terms that make 321-like orders especially easy. Stems, of course, amount to lexical bottoms of the relevant hierarchies, so a stem plus two suffixes (ordered according to the Mirror Principle) simply is a 321 order. Just like N-Adj-Num-Dem order in DPs, this ordering can be interpreted without any reordering; memory isn’t really required. By the same reasoning, (Mirror Principle compliant) prefixes on a stem represent a 123-like order: maximally loading memory, but easing the learning task of mapping morphemes to hierarchical positions.
Second, we can justify (some of) the correlation with overall clause order (which to my knowledge has only been approached before in terms of cross-categorial harmony). Consider, for example, an SOV language with a series of prefixes on the verb. Treating V as the lexical bottom of the clause hierarchy, this is an instance of 123 order; the S and O must be held in stack memory until the verb is encountered. But prefixes on the verb must also be held in memory before the verb, so the load on memory resources is maximal for this order. By contrast, for an SVO language, only the S adds to the additional memory load induced by the prefixes. And in verb-initial languages, there are no pre-verbal arguments adding to the memory load, making prefixing less of a memory problem.
This strikes me as an interesting approach… though a careful examination suggests complications. One surprising fact, from this point of view, is that SOV languages are the most common type, while VOS languages are quite exotic. While it’s appealing to conflate the avoidance of OSV as a basic clause order with 213-avoidance in other domains, I think that’s probably not correct, for reasons I detail below. Difficulties also arise in thinking about verbal morphology and DP arguments of the verb as part of a single hierarchy of the clause.