Conceptual motivation for Economy of (C-)Command
My thesis (Economy of Command) grew out of an attempt to understand the X-bar schema as something like an optimal packing solution. Such a claim invites the question, “what is X-bar optimized with respect to?” or, more simply, “what is it good for?”
The motivation I explored had to do with computational concerns in the abstract derivation of a sentence. It is well-established that a variety of linguistic dependencies are governed by c-command, which can be understood in terms of search operations accompanying structure-building. In one formulation, at the point when two syntactic objects X and Y are Merged, relations of various kinds can be established between the whole object X and Y, or constituents of Y, while Y as a whole may enter into relations with X, or constituents of X. This leads to structural restrictions on permissible relations, due to a derivational horizon on search.
One reasonable concern for computational operations is to limit the amount of work required. One measure of work done is the number and depth of search operations. Concerns of this sort loom large in the context of Chomsky’s Minimalist Program, which seeks to shift the burden of explanation for syntactic phenomena away from stipulated properties specific to linguistic cognition, to more general principles (of non-linguistic cognition, general computation, or even “natural law”). Put another way, the Minimalist expectation is that search operations in syntax should be minimized, all else equal.
It is a mathematical fact that some binary-branching arrangements of a given number of terminal elements yield more c-command relations than other arrangements of the same elements. This is illustrated with two trees with four terminals in the figure below.
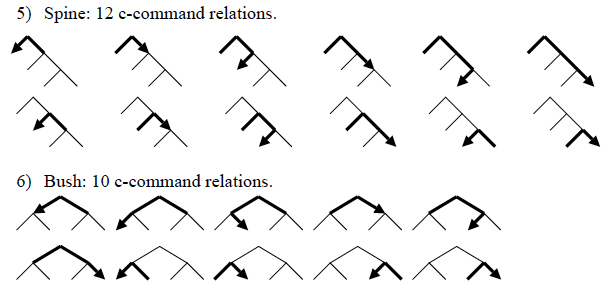
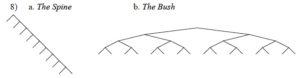
As it turns out, a unidirectionally-branching comb (the Spine) maximizes c-command relations, while a flat, shallow tree (the Bush) minimizes them. The difference in total c-command relations is small in small trees, but grows dramatically in larger structures.
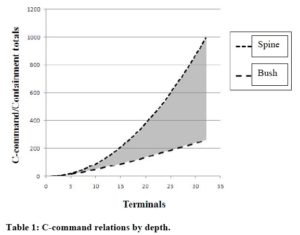
C-command relations are understood as reflecting iterated search operations accompanying structure-building, and the Minimalist Program leads us to suppose that search operations ought to be minimized if possible. It seems like a reasonable hypothesis that human syntactic structures ought to tend toward structures that minimize c-command relations (within the bounds of whatever other constraints such structures must satisfy), as such structures put a tighter limit on how much work might be required in the course of a derivation. Syntactic structures ought to economize on c-command relations; this is what I mean by Economy of Command.
The ideas I explored were new in detail, but echo in a general way the concerns that underlie several other approaches. Minimization of the length of individual c-command relations is seen in Relativized Minimality, for example. Chomsky’s recent work on his Labeling Algorithm singles out minimal search as the means of identifying the label of a given syntactic object. My work aligns with this approach in two ways: I agree that labels are not “on” syntactic objects but come about as a secondary effect, and minimal search is also the central tool I exploit, though casting my view beyond individual instances to derivations as a whole. Minimization of dependency length is also at the center of work such as Futrell, Mahowald & Gibson’s; the difference is that they are computing realized dependencies in terms of distance over surface order, while I am measuring the scaffolding of possible dependency paths in the abstract hierarchical structure.
Two applications of Economy of Command
My thesis explored two applications of this hypothesized preference for minimizing c-command relations. First, I claimed that phrase structure is shaped so as to satisfy this preference. Second, I claimed that syntactic movement is a means of reducing c-command relations.
Economy of Command in Phrase Structure
Pursuing some of the ideas mentioned on my Fibonacci & L-grammars page, I aimed to show that X-bar-like structure can be motivated in terms of minimizing c-command relations. The perspective I took was to consider the relevant phrase structural pattern as a matter of branching structure, totally divorced from any considerations of labeling and projection. The game is to suppose that we are trying to create structure for a discrete infinite system in some self-similar way, and to see what structural “habits” are best. I assumed that any such structure must be built bottom-up by binary Merge, with one or more characteristic sites for terminal elements, and slots for combination with more complex objects.
Looked at this way, the X-bar schema of Phrase –> [Specifier [Head Complement]] can be simplified to Phrase –> [Phrase [terminal Phrase]], where the instances of “Phrase” on the right-hand side of the rule are themselves built by the same template. Of course, there are other possibilities: at this level of description, there is no reason why a self-similar template for discrete infinite structure couldn’t have several terminals, or be built out of complex objects of a different character than the whole. One alternative pattern with equivalent local amounts of structure would be Phrase –> [terminal [Phrase Phrase]]. One might object that such a template is odd for linguistic use: its terminal, which we’re used to thinking of as the head of its projection, isn’t at the bottom, while two full phrases (of the same shape) combine symmetrically. But it’s precisely the point of this line of inquiry to try to explain familiar properties, such as headedness and projection, from more basic considerations.
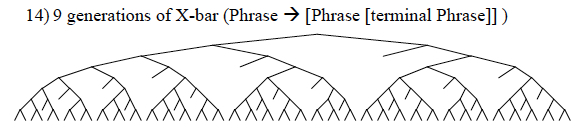
The diagram above illustrates what happens when we grow the X-bar format uniformly to a depth of 9 branching levels. Compare that to the diagram below, which is the result of uniform expansion of the alternative “high-headed small clause” pattern.
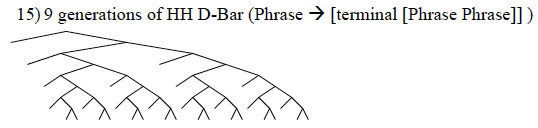
As is immediately obvious, the X-bar pattern grows a denser, bushier tree. As a consequence, building up syntactic structure from a fixed number of terminals according to the X-bar pattern creates fewer c-command relations than structuring the same amount of material according to the alternative pattern. This entails that there is a much tighter bound on the number and depth of search operations potentially computed, which I take to mean that the X-bar pattern is better.
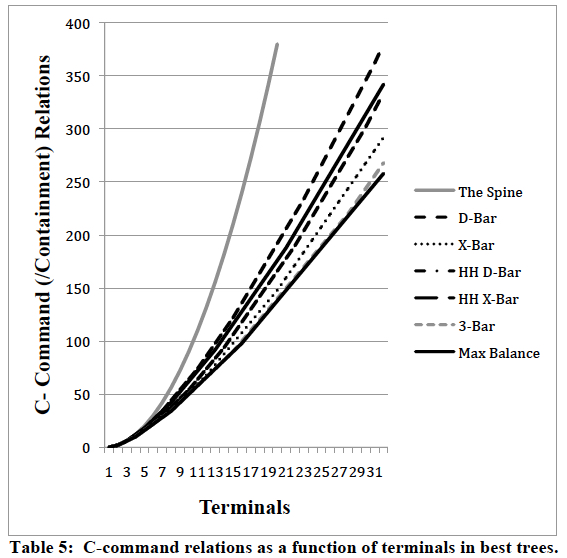
In fact, the X-bar schema is better at minimizing c-command relations than any alternative scheme of equivalent complexity. Now, still-better minimization can be achieved if we allow for schemes with greater internal complexity. For example, with patterns distinguishing three kinds of combination (where X-bar countenances two, corresponding to the X’ and XP levels of traditional X-bar theory), the best option is what I call 3-bar, which can be written as Phrase –> [Phrase [Phrase [terminal Phrase]]].
The best patterns look like projections
What emerges is that for any specified level of pattern complexity, the pattern that best minimizes total c-command relations looks like a generalized X-bar structure: a single terminal slot at the bottom of the pattern, combining at each subsequent level with another phrase isomorphic to the maximal phrase. This result is surprising, because those properties are in no way enforced by the rules of the game. I argued that this result might provide some insight into where projection/labeling comes from. Even if projection is not native to the syntactic combinatoric system, optimized syntactic combination should produce structures that look like projections, with a tendency for each maximal phrase to be built around a single designated “head” terminal at its bottom, with non-head daughters also maximal projections. Since labeling has proven difficult to motivate as a computational primitive, it is interesting that a basis for it might emerge for free, as an epiphenomenon of minimizing the domain of search operations.
Economy of command in syntactic movement
Those familiar with the recent literature, especially in syntactic cartography (what Heidi Harley jokingly calls “the Italian job”), may find reason to object already. Economy of command amounts to a preference for bushy, balanced trees, yet the cartographers claim that various syntactic domains are, at base, built from what I claim is the worst structure: a Spine. If language design were sensitive to minimizing c-command relations, why would this be so?
My answer to this objection has several layers. A first point is that the objection is simply mistaken: the base structure is a Spine when viewed as a projection of its head, but it is not really a unidirectionally-branching comb. Rather, in cartographic work substantive categories introduced along the Spine are often phrasal specifiers, with potentially complex branching structure of their own.
More importantly, there is reason to think that the number of c-command relations in the base structure is irrelevant. Many dependencies measured out by c-command incur their computational cost not within narrow syntax, but only at the interfaces, when syntactic structure is transferred to external systems for pronunciation and interpretation. An obvious case is linearization according to Kayne’s Linear Correspondence Axiom or related algorithms, which nowadays is standardly taken to apply only at Transfer. That view (of c-command computed at the interfaces) underlies Moro’s work on Dynamic Antisymmetry, where symmetry in unlinearizable base configurations can be broken by movement, and in Chomsky’s view of Criterial Freezing as a consequence of the Labeling Algorithm.
Movement can help
If what matters for computational optimization is the set of c-command relations present at the interfaces, then syntactic movement can serve to balance an unwieldy Spine. Concretely, let’s suppose that interface systems see only a truncated trace in the launching site of movement, with no visible internal structure. The abstract trees below, before and after movement of the object labeled D, demonstrate how movement can help: the after-movement structure (b) has fewer c-command relations than the before-movement structure (a), namely 38 instead of 42 total c-command relations.
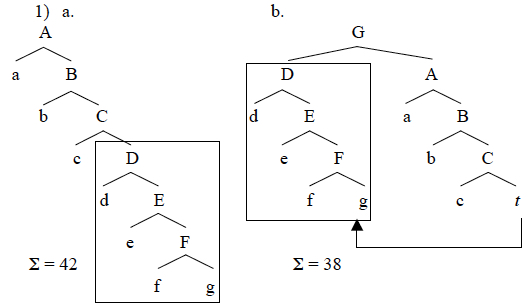
In fact, we might wonder if this is in fact the purpose of syntactic movement: what if it is a mechanism to reduce c-command relations? Although the goal is to reduce the total number of relations in the final objects delivered to the interfaces, achieving that goal would require complicated look-ahead. I assume instead that movement is triggered dynamically in the syntax without lookahead, and is possible just in case it reduces c-command totals at the derivational stage when it occurs.
The Fundamental Movement Condition
These assumptions allow us to be precise about the conditions that must hold to potentially trigger movement. Movement of syntactic object alpha to the edge of the containing category beta will reduce c-command totals iff the Fundamental Movement Condition (FMC) holds. The FMC is an inequality stated over three quantities: the total number of nodes in the moving and non-moving portions of the tree, and the pre-movement depth of the former in the latter.
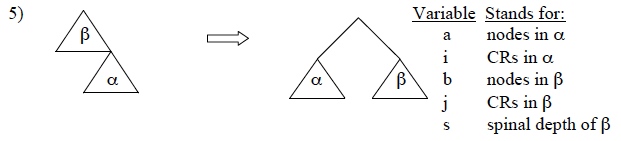
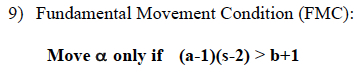
Applying this to the example from above: the moving and non-moving portions of the tree both have 7 nodes (a=b=7), and the spinal depth (counting nodes from A down to and including the trace of D) s=4. Plugging these into the FMC, we have (7-1)(4-2) > 7+1, or 12>8. This is true, so movement is possible — note that the margin by which the inequality is satisfied is just the difference in the number of c-command relations.
Some basic consequences
Just like my ideas about phrase structure, I tried to push this idea about movement to its limit, to see how much could be explained in just these terms, without incorporating the further technical machinery usually assumed for movement (such as features). It seems that some interesting conclusions can be drawn, which (with a healthy dose of charity and imagination) might explain some well-known properties and patterns of syntactic movement.
Anti-Locality
Right off the bat, we derive a form of Anti-Locality (a ban on too-local movement). Anti-Locality has been discussed in terms of featural motivations: if a phrase XP is complement to a head H, it is already visible and maximally local to that head; there can be no motivation for moving from complement to specifier within a single projection (see e.g. Abels 2003).
But effectively the same condition falls out from the FMC, repeated here: (a-1)(s-2) > b+1. In movement from complement to (first) specifier of the same head, the spinal depth s=2, so one of the factors on the left-hand side (s-2) is equal to zero. Then the entire left-hand side is equal to zero as well, and the inequality cannot be satisfied, regardless of the size of objects involved.
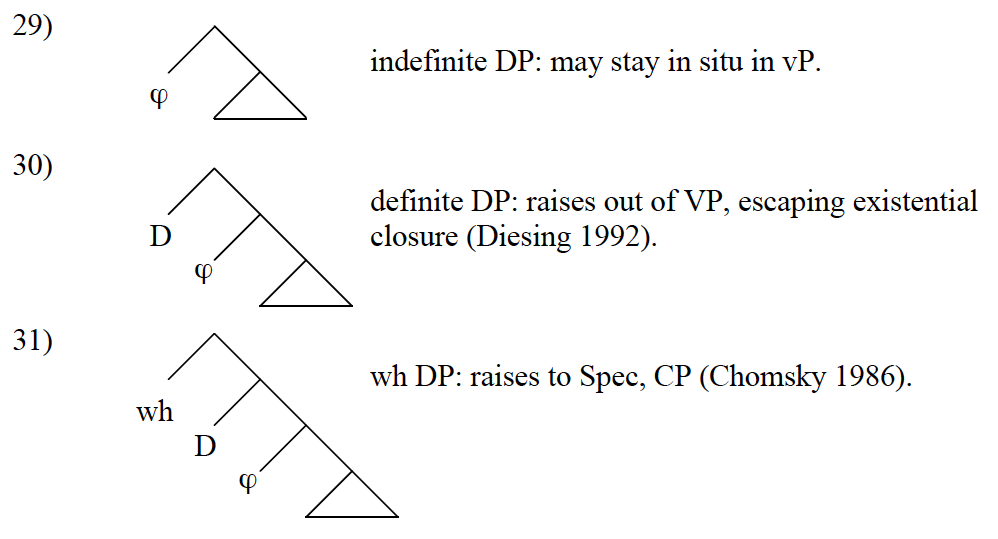
Differential DP movement
Another way of squeezing predictions out of the FMC is to consider what happens when we hold everything else constant, and vary the factor a, representing the size of the moving category. For a fixed embedding context, we derive a size threshold effect: a category that is too small cannot satisfy the condition, while a slightly larger category can, allowing it to move. I speculated that this might underlie Object Shift, if indefinites are smaller than definites (the former lacking a layer of functional structure that the latter possess). In a similar vein, we might attempt to account for why wh-phrases move to a position that does not attract other kinds of DPs, if they possess more functional structure.
A-bar and A-movement
Now let’s incorporate the notion of syntactic cycles or phases, and ask how that might affect observed movement patterns. If optimization is relativized to that level, it seems that the best movement is one that, all else equal, maximizes the factor s — the distance moved. Plausibly, this means moving something to the top of the phase, its edge: that’s the general profile of A-bar movement.
But notice that while such a movement may be the best possible within a single phase, it “passes the buck”, as it were, under the assumption that the phase edge remains visible to the next higher phase. Then the large moved category will be c-commanded by material in that higher phase, piling up c-command relations — and then we will have to move it again to balance the higher phase. This might take us some distance towards an understanding of successive-cyclic movement.
However, a more clever strategy, if it can be arranged, would be to move as far as possible within a phase without quite reaching the phase edge. Considerable reductions in c-command totals could be achieved, and by stopping just below the edge the large moving object is hidden from the higher phase, preventing the pile-up of further searches into its interior from above. That sounds rather like the profile of A-movement, such as EPP movement to the specifier of TP, or object movement to just below the edge of vP: as high as movement can go while not passing through to the next higher phase.
Roll-up movement
A further speculative step is to consider how movement operations might influence the conditions for subsequent movement. One interesting case is so-called roll-up movement, deployed in some analyses of head-final word orders. This is an extremely local form of movement (minimally Anti-Local) involving a kind of snowballing effect, moving a phrase to the left, then moving that phrase plus the element it inverted with, and so on, resulting in word order reversal.
Suppose that one stage of such movement has applied, inverting a piece of structure past a minimal dominating structure.
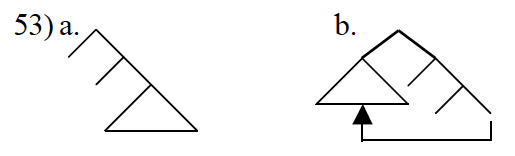
Now further material is Merged, and the slightly larger “snowball” inverts with a minimal dominating structure.
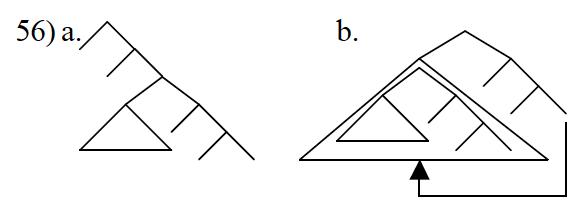
By hypothesis, the first step of movement satisfied the FMC. When the next step of roll-up movement occurs, two of the factors (non-moving tree size, and distance moved) in the FMC remain the same, but the moving category is strictly larger. This means that the reduction in c-command totals is successively greater for each next step of movement, giving a kind of positive feedback effect (like a snowball gathering momentum).
Universal 20
Needless to say, the effects motivated above are hand-wavy and speculative. I wanted to test my theory of movement against a reasonably nuanced data set, and decided to see if I could replicate the noun phrase ordering facts relevant to Greenberg’s Universal 20, as refined in Guglielmo Cinque’s (2005) work.
Universal 20 concerns the relative ordering of demonstratives, numerals, adjectives, and nouns, across languages. Greenberg’s original formulation of Universal 20 has been refined by further typological work; there is some debate about exactly which orders are or are not attested. Cinque claimed that 14 of the logically possible 24 orders are found, namely those derivable from a fixed bottom-up Merge order with non-remnant movements. Others describe the facts differently; Matthew Dryer, in careful work, claims to find 2 or 3 more orders than Cinque allows. As a fixed point of reference, I decided to run with Cinque’s characterization; the table below summarizes his claims about which orders are attested or unattested.
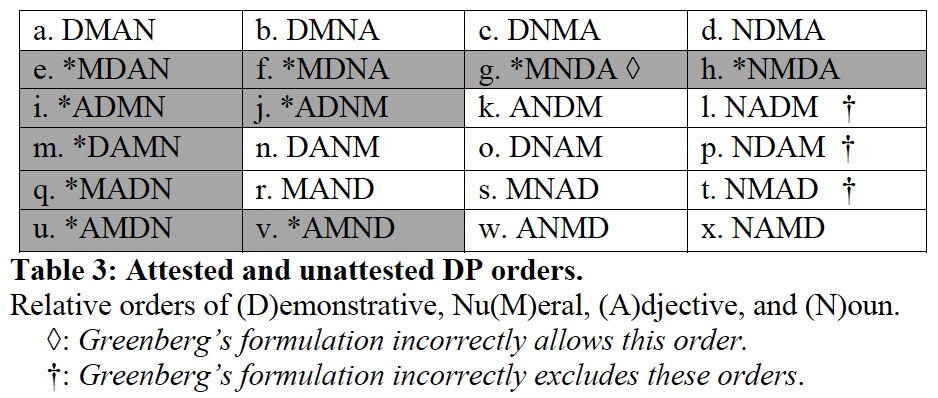
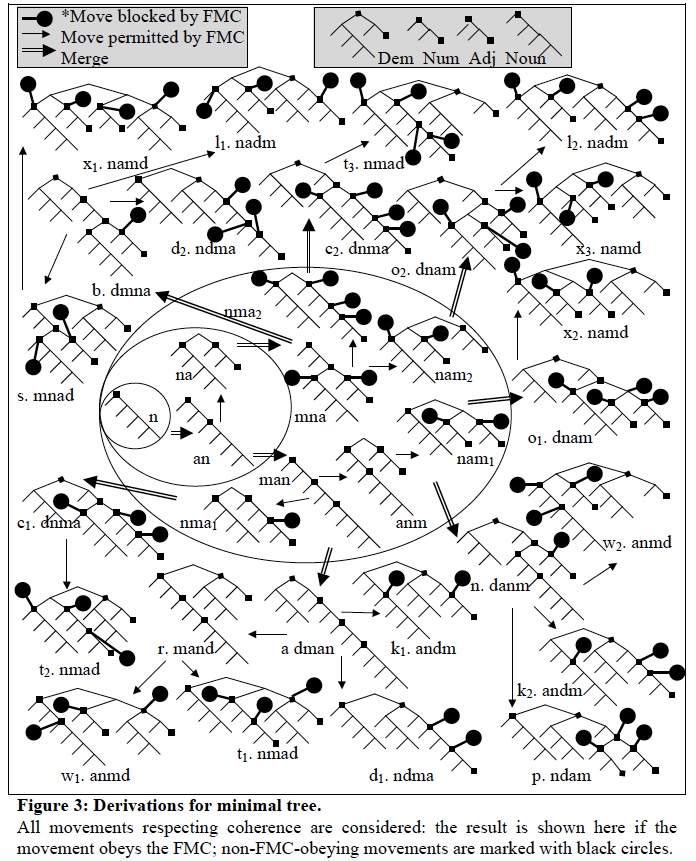
To put my ideas about movement to the test, I wanted to find out if there could be a single, universal DP tree, such that all and only the attested word orders (per Cinque) were derivable by FMC-licensed movements. This is a considerable abstraction, and I had to make some further somewhat dubious commitments to make the problem tractable. For example, I assumed that each overt category (demonstrative, numeral, adjective, noun) was “coherent”, not susceptible to being broken up by movement; only movements respecting coherence in this sense were considered. I also assumed that there were no accidental gaps in the typological paradigm: every derivable order was attested.
Even so, it was a painful amount of work to map out conceivable derivations. I worked out what seemed like all the structures reasonably derivable from movement, then all the movements that could reasonably proceed from there, and so on. For each attested order, I required that at least one derivation had each movement step satisfying the FMC, while requiring that no unattested orders had such an FMC-satisfying derivation. This yielded an enormous conjunction of inequalities over the same set of variables (representing the size and depth of the relevant categories in the supposed universal DP); the entire expression runs to more than a page in my dissertation.
Having done this, it was possible to work backwards to look for base trees that could underlie the possible and impossible orders. I wrote a simple Java program, which plugged in all possible values for the individual variables within a specified range, and checked for each case whether the conjoined movement condition was satisfied or not. The first goal was to see if such a base tree could be found at all; the second goal was to characterize the solution set, if it proved to be non-empty.
It worked! There are indeed trees that we can postulate as base DP structures, that would lead to all and only the attested word orders with all possible movements satisfying the FMC. To illustrate how this works, here is the smallest overall tree I found in the solution set:
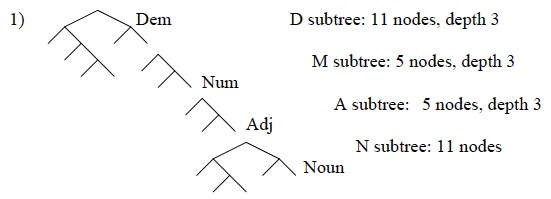
Supposing that this tree were the base structure for every language, we find that each attested order has one or more derivations in which every step of movement (if any) satisfied the FMC (i.e., reduced c-command totals as it applied). So, for example, the attested order noun-demonstrative-numeral-adjective (NDMA) requires one step of movement, which does indeed produce a more balanced tree.
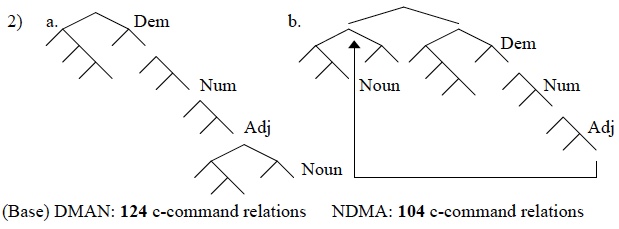
On the other hand, unattested orders like *Adjective-demonstrative-noun-numeral have no derivation where each step of movement is licensed by c-command reduction. One such “bad” derivation is below: the c-command totals after movement are greater than before movement, ruling it out.
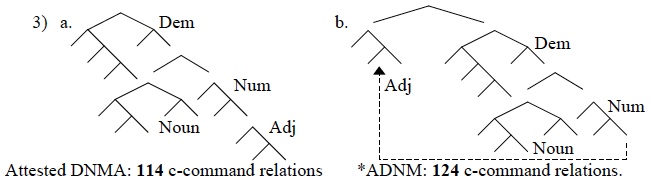
I was worried that I might have made an error somewhere in the grotesque amount of work I had done as background, figuring out possible movements and writing down conditions for each configuration. So I checked by hand, and was relieved to find that–at least for this smallest solution tree–I hadn’t made an error; the FMC-licensed movements do indeed lead to all and only the attested orders. This is demonstrated in the rather awful figure below.
Summing up
Running with the idea that c-command minimization mattered for syntax, for reasons having to do with minimizing search in an abstract computation, seemed to say some interesting things about what phrase structure ought to look like: it should be shaped like X-bar projections, even without a primitive notion of projection/labels. Hypothesizing that syntactic movement was a mechanism for reducing total c-command relations, I managed to derive some interesting results, plausibly in line with established properties of syntactic movement. Pushing the theory to its (or at least, my) limits, I even managed to show that it could account for the word order possibilities falling under Universal 20 and (one of) its modern refinements.
Now what?
It might be disappointing to hear that, for all the effort I poured into these ideas, I’ve since abandoned them completely. I don’t really believe that any of the preceding work is on the right track!
After finishing my dissertation, I continued to poke at the facts I had tried to explain. One day I noticed something about Cinque’s remnant-movement account of Universal 20… With just two elements, both possible orders can be derived. Of the 6 possible orderings of three elements, his system predicts that 5 are attested. With four elements, as in the Universal 20 case, his account yielded 14 attested orders.
2, 5, 14,… Those are the Catalan numbers! What were they doing hiding in syntax, and what could it mean? Well, one thing the Catalan numbers count are the so-called Dyck trees, and I discovered that Cinque’s trees were related to the Dyck trees in an obvious way. Chasing that down led me to reading about permutations avoiding forbidden subsequences, and thence to Knuth’s stack-sorting algorithm.
That led to my latest project: ULTRA, the Universal Linear Transduction Reactive Automaton. I’ve come to believe that not only was my dissertation barking up the wrong tree, but generative syntax as a whole has missed something important.